本文主要记录《机器学习实战》中的理论知识拓展和实践问题中解决方案的总结

大纲
- 决策树基础概念
- 建立简单决策树
- 使用隐形眼镜(真实数据)建立决策树
概念
分类树(决策树):是一种十分常用的监督学习分类方法。监督学习就是给定一堆样本,每个样本都有一组属性和一个类别,这些类别是事先确定的,那么通过学习得到一个决策树分类器,这个分类器能够对新出现的对象给出正确的分类。
决策树选择哪一个特征作为分类标准是依据信息熵,信息熵通俗来说就是数据集的不确定性、混乱程度,数据集的信息熵越高,则混乱程度越高,数据集越不纯洁,决策树根据遍历所有特征来拆分数据集,得出使得信息熵最低的子数据集的拆分特征,这个特征就是决策树选择分类标准的特征
根据简单的数据建立简单的决策树
首先创造一些简单的测试数据1
2
3
4
5
6
7
8
9
10
11
12from numpy import *
from math import log
# 创造一些测试数据
def createDataSet():
dataSet=[[1,1,'yes'],
[1,1,'yes'],
[1,0,'no'],
[0,1,'no'],
[0,1,'no']]
featureName=['no surfacing','flippers']
return dataSet,featureName
编写计算数据集信息熵的函数1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19# 香农熵:变量的不确定性(无序程度)越大,熵也就越大,数据集越混乱
# 计算给定数据集的香农熵 公式:对于所有可能的标签数求和-p(xn)*log2(p(xn))
def calShannoEnt(dataSet):
numRow=len(dataSet)
labelCounts={}
# 统计数据集最后一列标签列每个标签出现的次数
for item in dataSet:
label=item[-1]
if label not in labelCounts.keys():
labelCounts[label]=0
labelCounts[label] +=1
# 计算香农熵 求和-p(xn)*log2(p(xn))
shannoEnt=0.0
for key in labelCounts:
pxn=float(labelCounts[key])/numRow
shannoEnt-=pxn*log(pxn,2)
return shannoEnt
根据编写的计算信息熵的函数,可以通过遍历所有特征量拆分数据集来找到使得子数据集信息熵最低的特征1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30# 找到划分数据集后香农熵最低的特征的索引
def chooseBestSplitFeature(dataSet):
numFeature=len(dataSet[0])-1
beforeSplitShanno=calShannoEnt(dataSet)
bestInfoGain=0.0
bestFeature=-1
for i in range(numFeature):
# 计算这个特征有多少value
allValue=[item[i] for item in dataSet]
# 取集合去除重复项
uniqueValue=set(allValue)
# 计算特征i划分时的香农熵
splitShanno=0.0
for value in uniqueValue:
splitDataSet=[]
# 将dataSet中每项以特征i的value划分
for item in dataSet:
if item[i]==value:splitDataSet.append(item)
# 计算以特征i的值value划分的子数据集的香农熵
# 公式为子数据集的个数和总数据集的比例乘以子数据集的香农熵
splitRate=len(splitDataSet)/float(len(dataSet))
splitShanno+=splitRate*calShannoEnt(splitDataSet)
# 计算特征i划分时的香农熵与香农熵的差
# 差值越大证明熵下降不混乱度下降 数据集更纯洁
infoGain=beforeSplitShanno-splitShanno
if infoGain>bestInfoGain:
bestInfoGain=infoGain
bestFeature=i
return bestFeature
根据找到的这个特征,可以开始递归建树,以字典的形式保存二叉树,key为特征名, value为子节点(子树)
递归建树中的节点存在一个投票表决的停止过程,因此也需要编写投票表决函数1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55# 递归建树
# 停止条件:程序遍历完所有特征 或者 每个分支下的实例均具有相同的label
# 投票表决:若用完了所有特征有分支下的实例还不具有相同label则这个分支节点的分类属于多数实例的label
def voteLabel(dataSet):
# 对于每项的分类投票
classCount={}
for i in range(dataSet):
label=dataSet[i][-1]
classCount[label]=classCount.get(label,0)+1
# 返回最多的分类
count=0
maxLabel=''
for key in classCount:
num=classCount[key]
if(num>count):
count=num
maxLabel=key
return maxLabel
# 递归建树 返回子节点的类别名
def createDecisionTree(dataSet,featureName):
# 检测传入数据集的类别种类
allLabelValue=[item[-1] for item in dataSet]
uniqueLabel=set(allLabelValue)
# 集合数为1则证明传入数据集的类别相同 停止划分
if len(uniqueLabel)==1: return allLabelValue[0]
# 遍历完所有特征则返回数据集中出现次数多的类别
if len(dataSet[0])==1: return voteLabel(dataSet)
# 若还有特征可划分 则选择最好的特征划分数据集
bestSplitFeatureIndex=chooseBestSplitFeature(dataSet)
bestSplitFeatureName=featureName[bestSplitFeatureIndex]
decisionTree={bestSplitFeatureName:{}}
del(featureName[bestSplitFeatureIndex])
# 通过bestFeature的取值value将数据集分成子数据集
allSplitValue=[item[bestSplitFeatureIndex] for item in dataSet]
uniqueSplitValue=set(allSplitValue)
for value in uniqueSplitValue:
# 复制
subFeatureName=featureName[:]
# 按照bestSplitFeatureIndex和value划分数据集
splitDataSet=[]
for item in dataSet:
if item[bestSplitFeatureIndex]==value:
# 注意子数据集需要去除划分的feature
itemCopy=item[:]
itemCopy.pop(bestSplitFeatureIndex)
splitDataSet.append(itemCopy)
# 将划分的数据集填充到decisionTree中
# 递归建树
decisionTree[bestSplitFeatureName][value]=createDecisionTree(splitDataSet,subFeatureName)
return decisionTree
有了决策树字典,我们需要根据这个字典来预测未知数据的标签1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22# 使用决策树的分类
def classify(decisionTree,testVector,vectorFeatureName):
# 用于分类的特征
# py3中dict.keys()返回的是dict_keys,类似集合不能使用索引
splitFeature=list(decisionTree.keys())[0]
# print(splitFeature)
# 剩下的决策树
restTree=decisionTree[splitFeature]
# 在输入数据集中用于分类的特征的下标
featureIndex=vectorFeatureName.index(splitFeature)
for key in restTree.keys():
# 遍历到决策树正确路径
if testVector[featureIndex]==key:
# 判断是否是节点
if type(restTree[key]).__name__=='dict':
# 不是节点 继续遍历
classLabel=classify(restTree[key],testVector,vectorFeatureName)
# 是节点 则输出相应值
else: classLabel=restTree[key]
return classLabel
编写完所有函数后,我们可以开始测试简单数据,使用简单数据来构建一个决策树1
2
3
4
5if __name__ == "__main__":
dataSet,featureName=createDataSet()
featureNameCopy=featureName[:]
decisionTree=createDecisionTree(dataSet,featureNameCopy)
print(decisionTree)
运行查看构建的决策树
使用构建的决策树进行预测位置数据的标签1
2
3
4
5if __name__ == "__main__":
dataSet,featureName=createDataSet()
featureNameCopy=featureName[:]
decisionTree=createDecisionTree(dataSet,featureNameCopy)
print(classify(decisionTree,[1,1],featureName))
运行查看构建的预测结果
使用隐形眼镜的数据构建决策树
首先查看隐形眼镜的数据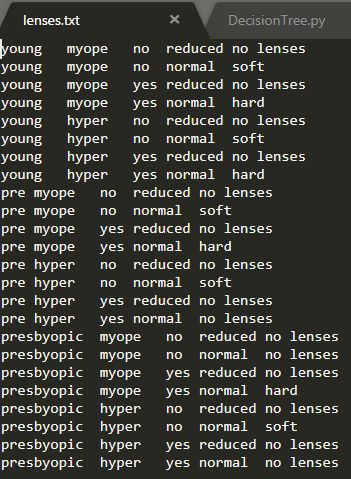
可以看到有4个特征,最后一列为标签值,我们先读取文件转换成数据集和创建特征名向量1
2
3
4
5
6# 读取隐形眼镜数据
def glassesDataSet():
fr=open('lenses.txt')
dataSet=[item.strip().split('\t') for item in fr.readlines()]
featureName=['age','prescript','astigmatic','tearRate']
return dataSet,featureName
由于有4个特征属于较多特征,决策树构建的过程比较耗时,我们可以将构建的决策树使用pickle序列化保存到本地,下次需要用可以直接读取,这样就不需要每次构建决策树
编写pickle序列化对象和读取文件转换成对象的方法1
2
3
4
5
6
7
8
9
10
11
12
13
14# 存储决策树:构建决策树比较耗时 可以使用pickle序列化对象在磁盘上保存对象
def storeTree(inputTree,fileName):
import pickle
# 打开方式需要加上b 二进制方式打开 因为pickle存储方式默认是二进制方式
fw=open(fileName,'wb')
pickle.dump(inputTree,fw)
fw.close()
def getTree(fileName):
import pickle
# 打开方式需要加上b 二进制方式打开 因为pickle存储方式默认是二进制方式
fr=open(fileName,'rb')
return pickle.load(fr)
根据隐形眼镜数据集构建决策树并序列化保存1
2
3
4
5
6
7
8if __name__ == "__main__":
# 使用决策树预测隐形眼镜类型
# 隐形眼镜数据
dataSet,featureName=glassesDataSet()
# 创建决策树并保存
featureNameCopy=featureName[:]
decisionTree=createDecisionTree(dataSet,featureNameCopy)
storeTree(decisionTree,'lensesDecisionTree.txt')
读取保存的决策树文件并打印出构建的决策树1
2
3if __name__ == "__main__":
decisionTree=getTree('lensesDecisionTree.txt')
print(decisionTree)
运行并查看结果