
本文记录剑指Offer中的50道面试题及一些个人个人拓展
大纲
- 面试题 1:赋值运算符函数
- 面试题 2:实现Singleton(单例)模式
- 面试题 3:二维数组中的查找
- 面试题 4:替换空格
- 面试题 5:从尾到头打印链表
- 面试题 6:重建二叉树
- 面试题 7:用两个栈实现队列
- 面试题 8:旋转数组的最小数字
- 面试题 9:斐波那契数列
- 面试题 10:二进制中1的个数
- 面试题 11:数值的整数次方
- 面试题 12:打印1到最大的n位数
- 面试题 13:在O(1)时间删除链表结点
- 面试题 14:调整数组顺序使奇数位于偶数前面
- 面试题 15:链表中倒数第K个结点
- 面试题 16:反转链表
- 面试题 17:合并两个排序的链表
面试题 1:赋值运算符函数


赋值运算符函数基础4要数:
1.返回值类型声明为该类型的引用并在函数结束前返回实例自身引用:只有这样才能实现连续赋值运算
2.参数类型声明为常量引用:常量是因为在函数体内不改变传入实参状态,引用是可以减少一次从形参到实参的复制构造函数的调用,节省空间开销提高代码效率
3.释放实例自身已有内存:在分配新内存之前释放已有空间,避免内存泄露
4.需要判断传入参数和当前实例(*this)是不是同一个实例:若是同一个则不进行赋值直接返回,若没有判断则在释放实例自身内存时传入的参数的内存也被释放了,就再也找不到需要赋值的内容了
结合以上4点的解法1
2
3
4
5
6
7
8
9
10
11CMyString& CMyString::operator =(const CMyString &str) //返回值+参数(1.2.)
{
if(this == $str) return *this; //判断是否是自身赋值自身(4.)
delete []m_pData; //被赋值的实例的成员变量delete释放内存(3.)
m_pData = NULL; //初始化变量
m_pData = new char[strlen(str.m_pData)+1]; //new分配内存
strcpy(m_pData,str.m_pData); //赋值
return *this; //返回自身实例用于连续赋值运算(1.)
}
考虑异常安全性:若new char时内存不足导致抛出异常,m_pData将是空指针,程序十分容易崩溃,此时由于被赋值的实例的成员变量已经被delete了,实例改变了自身的状态,违背了异常安全原则。
解决方案:
1.先new分配内存再delete释放内存,当new失败时我们能确保实例不会被修改原先状态
2.先创建一个临时实例,再交换临时实例和原来的实例,如下1
2
3
4
5
6
7
8
9
10
11
12
13
14CMyString& CMyString::operator =(const CMyString &str)
{
if(this != $str)
{
CMyString strTemp(str); //调用复制构造函数新创建一个临时实例
char* pTemp = strTemp.m_pData; //利用一个中间变量pTemp将变量值交换
strTemp.m_pData = m_pData;
m_pData = pTemp;
}
//在if作用域外,由于strTemp是局部变量会自动调用析构函数释放内存,
//其中strTemp中的成员变量m_pData所指向的内存就是原来被赋值实例成员函数的内存,刚好一并释放
return *this;
}
面试题 3:二维数组中的查找

一般的思路是从左上角开始做比较,但是减小排除的范围无规律,若是从右上角或者左下角做比较,则可以以行或者列减小排查范围,而二维数组以连续内存存储的特性让我们可以通过下标访问数组以矩阵形式的空间位置。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23bool Find(int* matrix, int rows, int columns, int number)
{
bool found = false;
if(matrix != NULL && rows >0 && columns >0) //矩阵有效性检测(若输入空指针)
{
int row = 0;
int column = column -1;
while(row < rows && column >=0) //循环停止条件:最后一行或者第一列
{
if(matrix[row * columns + column] == number) //第row行第column列,相当于[row][column]
{
found = true;
break;
}
else if(matrix[row * columns + column] >number)
column--;
else row++;
}
}
return found;
}
面试题 4:替换空格

网络编程中,URL参数中特殊字符串(空格、#等)需要替换成服务器端可以识别的字符,转换的规则是在’%’后面加上字符ASCII码的两位十六进制表示,如空格的ASCII码为32,十六进制为0x20,因此空格被替换成”%20”。
解题思路:题目理解有两种,第一种是创建新的字符串并在新的字符串上做替换,则我们可以分配足够多的内存,第二种是在原字符串上做替换,则我们需要保证输入字符串后有足够多的空余内存并且不能覆盖原字符串的内存。
解法一:字符串从前往后遍历找到一个空格则空格后的字符集体向后移动两个字节大小。时间复杂度为O(n^2),多次移动次数,不是好的解决方案。
解法二:先遍历一次字符串,统计出字符串中空格总数由此计算出替换后字符串的长度,之后从字符串末尾开始复制和替换,这样所有字符只移动一次,算法的时间效率是O(n)。
具体的复制和替换过程为使用两个指针1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42void ReplaceBlank(char string[], int maxLength)
{
if(string == NULL && length <= 0) //输入参数有效性检测性
return;
//originalLength为字符串原先长度
int originalLength = 0;
int numberOfBlank = 0;
int i = 0;
while(string[i] != '\0')
{
originalLength++;
if(string[i] == ' ') numberOfBlank++;
i++;
}
//newLength为替换后的字符串长度
int newLength = originalLength + numberOfBlank * 2;
if(newLength > maxLength) //如果替换后字符串长度大于字符串总容量
return;
int indexOfOriginal = originalLength;
int indexOfNew = newLength;
while(indexOfOriginal >= 0 && indexOfNew > indexOfOriginal)//替换完成条件
{
//若是空格则后面的标记添加并前移三个字节
if(string[indexOfOriginal] == ' ')
{
string[indexOfNew --] = '0';
string[indexOfNew --] = '2';
string[indexOfNew --] = '%';
}
else
{ //若不空格则复制前面指针的字符到后面指针的位置,并前移指针
string[indexOfNew --] = string[indexOfOriginal];
}
-- indexOfOriginal;
}
}
面试题 5:从尾到头打印链表

面试中如果我们打算修改输入数据,最好先问面试官允不允许。
若允许我们可以将链表中的节点指针反转改变链表方向就可以了。
通常打印是一个只读操作,假设面试官要求这个题目不能改变链表结构。
思路:遍历是从头到尾,输出却是从尾到头,这是典型的后进先出的栈结构,然后递归的本质就是栈结构,于是我们可以每访问一个节点先递归输出它后面的节点,再输出该节点自身。
显示用栈调用代码如下1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19//Reversingly-倒置地
void printListReversingly(ListNode* pHead) //不用改变头指针,可传值
{
std::stack<ListNode*> nodes;
ListNode *pNode = pHead;
while(pNode != NULL)
{
node.push(pNode); //入栈
pNode = pNode->Next;
}
while(!node.empty())
{
pNode = nodes.top(); //取栈顶元素
cout << pNode->Value << endl; //输出节点值
nodes.pop(); //弹出栈顶元素
}
}
基于递归的栈调用代码如下1
2
3
4
5
6
7
8
9
10//Recursively-递归地
void printListReversinglyRecursively(ListNode* pHead) //不用改变头指针,可传值
{
if(pHead != NULL) //判断是不是空链表
{
if(pHead->Next != NULL) printListReversinglyRecursively(pHead->Next); //判断是不是最后一个结点,若是最后一个结点则递归结束
cout << pHead->Value << endl;
}
}
Tips:链表长时,导致函数调用层级很深,有可能导致函数调用栈移除,鲁棒性(程序稳定性)不好。
面试题 6:重建二叉树

思路:前序遍历可以确定树的根节点(第一个数字),中序遍历在知道了根节点的值后可以知道左子树的结点值(根节点左边的所有值)和右子树的结点值(根节点右边的所有值),之后用递归的方式完成剩下子树的建立1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49//树的主构造函数
BinaryTreeNode* Construct(int* preorder, int* inorder, int length)
{
if(preorder == NULL || inorder == NULL || length <= 0) //输入有效性检测
return NULL;
return ConstructCore(preorder, preorder+length-1, inorder, inorder+length-1);
}
//树的核心构造函数,通过传入前序遍历的头尾指针、中序遍历的头尾指针递归建树
BinaryTreeNode* ConstructCore(int* startPreorder, int *endPreorder, int* startInorder, int* endInorder)
{
//前序遍历的第一个数字是根节点的值
int rootValue = startPreorder[0];
BinaryTreeNode* root = new BinaryTreeNode();
root->m_nValue = rootValue;
root->m_pLeft = root->m_pRight = NULL;
if(startPreorder == endPreorder)
{
//若是输入的树前序只有一个值、中序也只有一个值且这两个值是同一个值
//则输入的这个值就是这棵树的根节点,否则是无效输入
if(startInorder == endInorder && *startPreorder == *startInorder) return root;
else throw std::exception("Invalid input");
}
//在中序遍历中找到根节点的值
int* rootInorder = startInorder;
while(rootInorder <= endInorder && *rootInorder != rootValue) rootInorder++;
//如果找到的节点在中序的末尾且值并不是根节点的值,返回错误
if(rootInorder == endInorder && *rootInorder != rootValue)
throw std::exception("Invalid input");
//可以通过找到的节点确定左子树长度和左子树范围
int leftLength = rootInorder - startInorder;
int* leftPreorderEnd = startPreorder + leftLength;
if(leftLength >0)
{
//构建左子树
root->m_pLeft = ConstructCore(startPreorder+1,leftPreorderEnd,startInorder,rootInorder-1);
}
if(leftLength < endPreorder-startPreorder)
{
//构建右子树
root->m_pRight = ConstructCore(leftPreorderEnd+1,endPreorder,rootInorder+1,endInorder);
}
return root;
}
让我们来看看ConstructCore做了什么事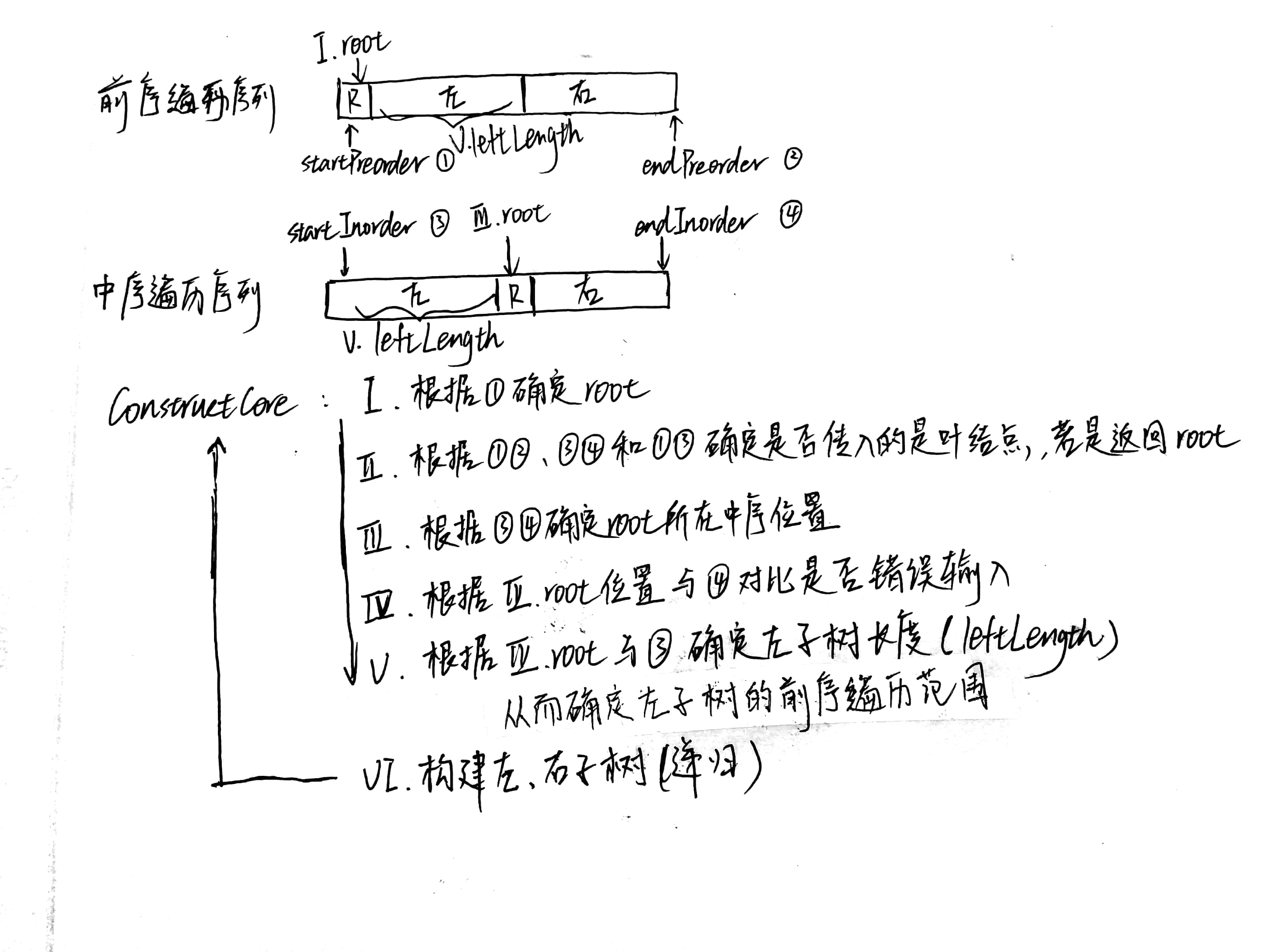
面试题 7:用两个栈实现队列

思路:插入元素直接插入第一个栈即可,删除元素则若是第二个栈有元素就pop,若是第二个栈没有元素,则将第一个栈的元素全部pop并push进第一个栈,之后按照第二个栈有元素的方式pop1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27//元素入队
template<typename T> void CQueue<T>::appendTail(const T& element)
{
stack1.push(element);
}
//元素出队
template<typename T> T CQueue<T>::deleteHead()
{
if(stack2.size() <= 0) //stack2空则将stack1全部弹出压如stack2
{
while(stack1.size() > 0)
{
T& data = stack1.top();
stack1.pop();
stack2.push(data);
}
}
//此时若是stack2还是空,则证明队列是空的
if(stack2.size() = 0) throw new exception("queue is empty");
T head = stack2.top(); //否则弹出栈顶元素
stack2.pop();
return head;
}
两个栈实现一个队列像是一个是插入栈一个是删除栈,而两个队列实现一个栈呢?
思路如下
面试题 8:旋转数组的最小数字

输入:{3,4,5,1,2}为数组{1,2,|3,4,5}的旋转
输出:1
思路:
- 1.直接遍历:时间复杂度为O(n),但没有利用旋转数组的特性
- 2.二分查找法:将数组看成两个递增数组,设置两个指针指向第一个元素p和最后一个元素q,由于一开始的数组为递增数组,则array[p]>=array[q],此时中间元素m若大于array[p]则为前部分递增数组的元素于是将p=m,中间元素若小于array[q]则为后部分递增数组的元素于是将q=m,不断逼近两个递增数组的交界元素,最后若p=q-1则找到了数组交界,此时array[q]为最小元素/array[p]为最大元素
- 3.特殊情况:若array[p]==array[q]==array[m]则无法确认arrary[m]属于哪部分数组,这种情况如下,需要使用顺序查找
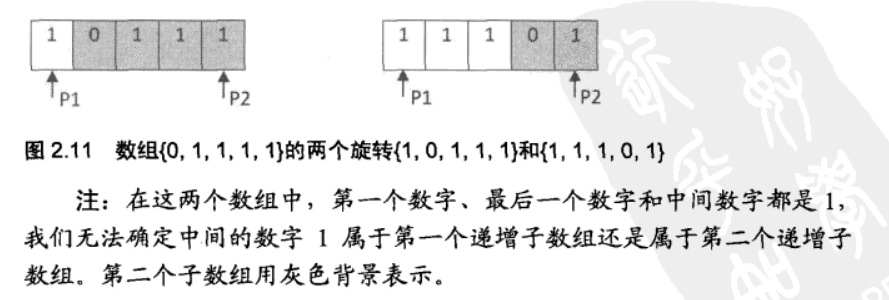
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35//二分查找
int Min(int array[],int length)
{
//输入有效性检测
if(array==NULL || length<=0) throw new std::exception("Invaild parameters");
int p=0;
int q=length-1;
//m初始化为0,因为若旋转数组是将0个元素放在后面,最小元素则为第一个元素
int m=0;
while(array[p]>=array[q])
{
if(q-p==1){
m=q;
break;
}
m=(p+q)/2;
//若array[p]==array[q]==array[m]转为顺序查找
if(array[p]==array[q] && array[m]==array[p]) return MinInOrder(array,p,q);
if(array[m]>=array[p]) p=m;
else q=m;
}
return array[m];
}
//顺序查找
int MinInOrder(int array[],int p,int q)
{
int result = array[p];
for(int i=p+1;i<=q;i++)
{
if(array[i]<result) result = array[i];
}
return result;
}
面试题 9:斐波那契数列
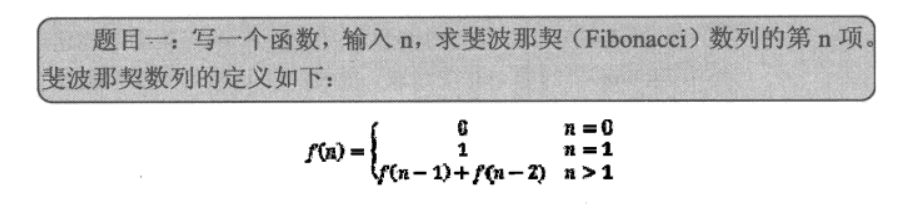
若用递归很简单1
2
3
4
5
6int Fibonacci(int n)
{
if(n<=0) return 0;
else if(n==1) return 1;
else return Fibonacci(n-1)+Fibonacci(n-2);
}
递归实现的效率十分低,而且设计大量的重复计算,如计算F(10)要计算F(9)+F(8),而计算F(9)又要计算F(8)+F(7),这样F(8)就重复计算了
1 | int Fibonacci(int n) |
改进2:改进1虽然避免了重复计算,但是空间开辟了太大,我们只需要得到F(n)不关心中间项的结果,因此中间项我们不必保存下来
1 | int Fibonacci(int n) |
—
面试题 10:二进制中1的个数

思路1::1的二进制为0…01,即除了第一位为1其他位均为0,利用这点,任何数与1作与运算,若其第一位为1,则运算结果为1,其第一位为0,则运算结果为0,之后可利用右移运算符验证下一位数直到所有数为0
思路1有一个问题是负数右移运算左边补的不是0而是1保证负数性质,因此最后数字会变成1….1陷入死循环
思路2::利用将1左移可避免死循环
1 | int numberOfNum(int n) |
思路2的问题是效率太低,有多少位的整数就要循环移动多少次
思路3::改变原来的数,消除输入数中的1,输入数中至少有一个1,若为xxx1000,则减1为xxx0111,此时减去的数与输入数做与运算,得到的结果是xxx0000,与输入数相比我们消除了其右边第一个1,继续使用这种方法直到输入数所有1被消除为0时停止
1 | int numberOfNum(int n) |
总结:把一个整数减去1之后再和原来的整数做与运算,得到的结果相当于把原来整数的二进制表示中的最右边的1变成0,即xxx100 & xxx011 = xxx000
面试题 11:数值的整数次方

类似于实现pow函数功能
思路1:使base与自身相乘循环exponent次数,缺点输入指数为0或者负数无法执行
思路2:负数时,可以对指数求绝对值,算出base的次方结果后再取倒数,当然要注意底数base是0的情况,0求倒数程序会运行出错,这时可以使用抛出异常处理
1 | double Power(double base,int exponent) |

思路3:当exponent较大时,pow函数中循环需要做多次乘法,可以优化一下乘方运算,用如下公式求a的n次方
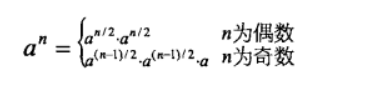
1 | double pow(double base,unsigned int exponent) |

—
面试题 12:打印1到最大的n位数

陷阱:大数问题,没有规定n的范围,若n位数大于整型(int)或者长整型(long long)时会溢出
思路1:在字符串上模拟数字加法,
1.申明一个长度为n+1的字符串(最后一个是结束符号’\0’),将字符串中数字初始化为’0’
2.字符串数字加法函数
3.打印字符串函数
1 | void PrintToMaxDigits(int n) |
面试题 13:在O(1)时间删除链表结点

思路1:从头指针遍历到结点指针的上一个指针,之后将上一个指针的Next指向结点指针的Next指针指向的结点即可,之后在链表中删除该结点,由于是顺序查找,时间复杂度为O(n)不符合要求
思路2:将结点指针的下一个指针的内容复制到需要删除的节点上,再把下一个指针删除,注意有两种特殊情况
1.结点指针是尾指针:此时没有下一个指针,因此还是需要顺序查找从头遍历
2.链表中只有一个结点:我们要删除的也是这个结点,这种情况我们删除掉结点后还要把链表的头结点设置为NULL
1 | void deleteNode(ListNode** pListHead,ListNode* pToBeDelete) |
时间复杂度:
对于n-1个非尾节点,为O(1);
对于尾节点,为O(n);
平均为[(n-1)*O(1)+O(n)]/n,结果还是O(1);
面试题 14:调整数组顺序使奇数位于偶数前面

思路1:维护数组的两个头尾指针,头指针向后移动直到遇到偶数停下,尾指针想前移动直到遇到奇数停下,若停下时头指针在尾指针前面则交换两个指针的值继续移动,否则停止移动调整数组顺序完成
1 | void ReorderArray(int* array,int length) |
思路2:解耦,可将判断条件封装成一个函数,即可拓展成许多情况,如将正数放在负数前面,将3整除的数放在3不整除的数,如快速排序中的分区函数比基准数小的数放在比基准书大的数的前面
1 | void ReorderArray(int* array,int length,bool (*func)(int)) |
面试题 15:链表中倒数第K个结点

思路1:由于是单向链表,因此无法从尾到头遍历,我们要找倒数第k个结点,若是知道链表中共有n个结点(尾节点为第n-1个结点),则找的是n-(k-1)就是第n-k+1个结点;我们可以定义两个指针指向头指针,由于倒数第k个结点的指针与尾指针相差k-1个结点,则让第一个指针先走k-1个结点,之后两个指针同时向后走,第一个指针走到尾节点时,第二个指针与其也相差k-1个结点,即是倒数第k个结点
鲁棒性检测
1.头指针为空指针
2.链表总数小于k
3.输入k为0
1 | ListNode* findKToTail(ListNode* head,int k) |

面试题 16:反转链表
思路:两个指针反转会出现链表断裂,因此需要三个指针,具体操作为前指针,当前指针,后指针,当前指针指向前指针,当前指针变前指针,后指针变当前指针,当前指针的Next指向为后指针,直到当前指针为尾指针,反转后变成头指针
陷阱:
1.考虑输入的头指针为NULL情况
2.输入的链表仅有一个节点的情况
3.输入的链表仅有两个结点的情况
4.原先头结点的Next变为NULL,头指针指向原先的尾节点
1 | ListNode* reverseList(ListNode* head) |
面试题 17:合并两个排序的链表

思路:类似于归并排序中的并过程,两个子数组通过两个指针比较大小值小的放在一个新数组,直到一个数组的值被遍历完之后另一个数组所有值被复制到新数组的后边
链表合并也是如此
1.新建一个头指针head和当前指针now指向头指针
2.新建两个指向子链表头结点的指针p和q
3.循环比较 *p和 *q的大小,值小的赋给now->Next,now->Next=p(q),之后p(q)=p(q)->Next;now=now->Next;
4.直到p(q)=NULL时,将now->Next=q(p)就完成了
1 | struct ListNode |
面试题 18:树的子结构

思路:
1.找到树1中与树2根节点的值相同值的结点
2.递归判断是否两个相同值的结点有相同的树结构
3.否则继续递归遍历其他根节点
1 | struct BinaryTreeNode |
面试题 19:二叉树的镜像

1 | //二叉树结点定义结构 |
思路: 画图可以发现,求树的镜像实质就是
1.前序遍历(根-左-右)树的每个结点
2.遍历到的结点是非叶子节点(有子节点)则交换两个子节点
1 | void MirrorTree(BinaryTreeNode* root) |
面试题 20:顺时针打印矩阵


思路:通过画图我们知道
1.循环打印的圈数是由矩阵matrix[x][y]中的较小的值决定的,并且每次开始循环打印的坐标点都是(start,start),综合我们知道循环继续的条件是start*2<x并且start*2<y
2.打印一圈可分解成四步:

3.关于二位数组传参问题,可参考这里,下面的程序其实会执行出错,因为访问number[i][j]需要使用(int*)number+i*columns+j的方式访问,处于程序清晰思路才写成如下访问方式
1 | void printMatrix(int** numbers,int rows,int columns) |
面试题 21:包含min函数的栈

思路:建立一个辅助栈存储当前栈中的最小值
1.若压入栈的数字大于之前栈中的最小值,则辅助栈压入之前栈中的最小值,
2.若压入栈的数字小于之前栈中的最小值,则辅助栈压入当前的最小值
1 |
|
Tips:编写代码时的两个小错误
1.不可用min()命名函数,与系统函数名冲突
2.函数模板的使用函数模板是根据传入参数推测出数据类型,因此不能自动推导返回参数类型,要做到自动推到返回参数类型,可使用
- 2.1 多次显示使用特定返回值类型重载函数,如 int minFunc(),double minFunc()
- 2.2 使用template
面试题 22:栈的压入、弹出序列

思路:
检测1:面对弹出序列的下一个弹出数字,若压入栈的栈顶元素是下一个弹出数字,则弹出
检测2:若下一个弹出数字不在栈顶,则继续将压栈序列中还没有入栈的数字压入,再次执行检测1
检测3:若所有数字都压入栈了仍然没有找到下一个弹出数字,则该序列不可能是一个弹出序列
1 | bool isPopOrder(const int* pushOrder,const int* popOrder,int length) |
面试题 23:从上往下打印二叉树

1 | //二叉树结点定义结构 |
思路:通过举例可以发现,打印结点的顺序是一个队列
1.将跟结点放入队列
2.打印队列头部的一个结点,若该结点有子节点,就将其左右结点放在打印队列的末尾,
3.重复打印队列头部的结点操作,直到队列中没有结点元素
Tips.小技巧:STL提供了两端可以进出的队列deque
1 | void printFromTopToBottom(BinaryTreeNode* root) |
技巧:广度优先遍历一个图还是一棵树,都要用到队列

面试题 24:二叉搜索树的后序遍历

1 | //二叉树结点定义结构 |
解题思路:递归+后续遍历特点+二叉搜索树特点
1.后序遍历中,序列最后一个数字为根结点的值
2.二叉搜索树中,左子树的值小于根节点的值,因此序列中前部分小于根节点的值的数为左子树的值
3.二叉搜索树中,右子树的值大于根节点的值,因此序列中后部分大于根结点的值的树为右子树的值
4.基于2.3.找到左子树和右子树序列,并判断左右子树中的值是否符合二叉搜索树规则
5.递归遍历左右子树
1 | bool verifySquenceOfBST(int array[],int start,int end) |

针对后序遍历可以使用两种方式实现
思路1:通过举例可以发现可以使用递归+栈的形式实现。
1.将当前遍历到的结点存入栈中
2.递归遍历右子树结点
3.递归遍历左子树结点
1 | static stack <int>backOrderStack; |
思路2:通过举例可以发现可以使用递归+队列的形式实现。
1.递归遍历左子树结点
2.递归遍历右子树结点
3.将当前遍历到的结点存入队列中
1 | static std::deque<int> backOrderQueue; |
面试题 25:二叉树中和为某一值的路径

解题思路:前序遍历特点+递归+栈
1.由于路径是从根节点出发到叶节点,二叉树遍历中只有前序遍历是首先访问根节点的
2.遍历到一个结点时是不知道父节点是什么值的,因此遍历的时候要保存结点
3.通过举例可以发现,若遍历到子节点这个路径加起来不是某一值时,要回溯到上一个结点,这是利用了递归的思想
4.此时要在保存结点计算路径值的和中删除掉这个结点,重新加上后面遍历的结点,因此保存结点的数据结构实际上是一个栈,因为递归调用的本质就是一个压栈和出栈的过程
1 |
|
面试题 26:复杂链表的复制

1 | struct ComplexListNode |
解题思路:拆分:1.插入新节点+2.建立sibling连接+3.拆分
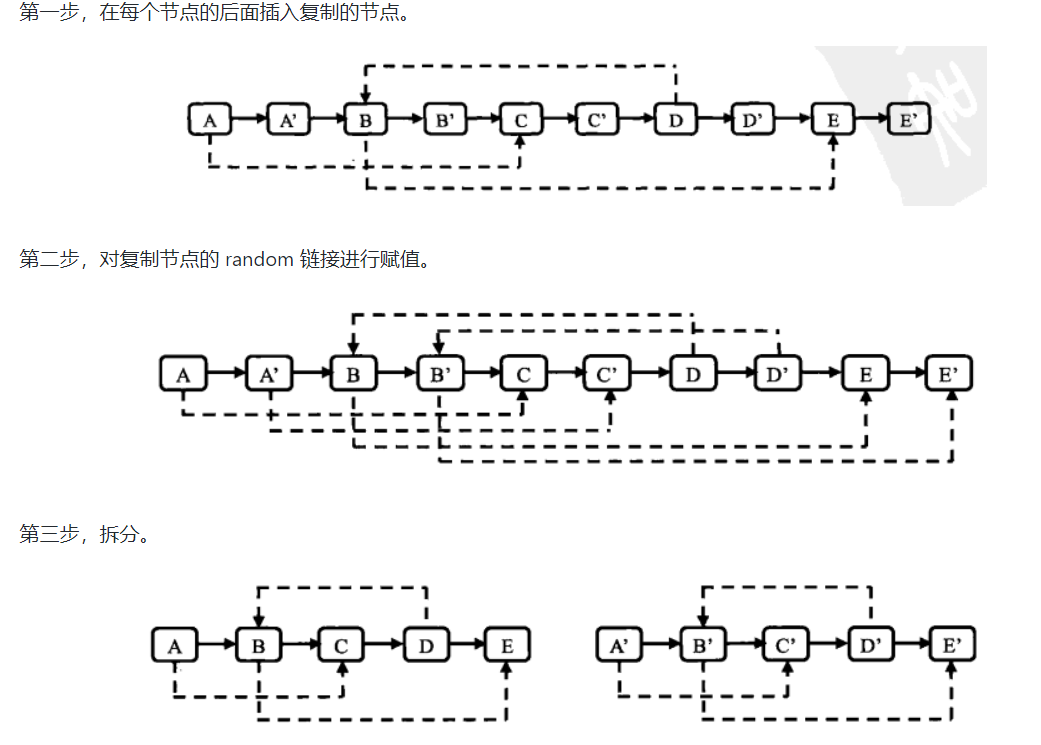
1 | ComplexListNode* cloneComplexListNode(ComplexListNode* head) |
面试题 27:二叉搜索树与双向链表


解题思路:搜索树特点+中序遍历+vector存储
1.搜索树特点+中序遍历:结合搜索树特点,根节点的值大于左子树的值小于右子树的值,使用中序遍历刚好遍历的结点符合这个规律
2.vector存储:使用vector将中序遍历的节点存储之后再进行相应处理

1 | vector<BinaryTreeNode*> inOrderVector; |
面试题 28:字符串的排列

解题思路:
面试题 29:数组中出现次数超过一半的数字
解题思路:摩尔投票算法
对于大多数投票问题,可以采用摩尔投票算法(Boyer-Moore Majority Vote Algorithm ),使得时间复杂度为 O(n)
摩尔投票算法:
1.设置变量majority存储多数元素和count存储此元素的投票数
2.遍历数组,若count=0,则majority设为当前数组元素,count++
3.遍历数组,若count!=0,则比较majority与当前数组元素,若相等则count++,若不相等则count–
4.检测:若数组中超过半数的元素值不存在,则majority返回随机一个元素,因此需要检测1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24int moreThanHalf(int* array,int length)
{
//有效性检测
if(array==NULL || length<=0) throw new exception("input is invalid!");
//摩尔投票算法
int majority=array[0],count=1;
for(int i=1;i<length;i++)
{
if(count!=0){
if(majority==array[i]) count++;
else count--;
}else{
majority=array[i];
count=1;
}
}
//4.检测
count=0;
for(int i=0;i<length;i++)
{
if(majority==array[i]) count++;
}
return count>length/2?majority:0;
}
面试题 30:最小的K个数
解题思路:快速排序中的分区函数/容器思想
1.对输入的n个数排序:排序之后位于最前面的k个数就是最小的k个数,时间复杂度为O(nlongn)
2.快速排序中的分区函数:有限制条件,只有允许修改输入数组时可用,基于第k个数来调整,使比k个数字小的所有数字位于数组左边,比k个数字大的数字位于数组右边,这样数字左边的k个数字就是最小的k个数字(乱序)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36int Partition(int* input,int start,int end) //分区函数
{
int i=start,j=end,x=input[start];
while(i<j)
{
while(i<j && input[j]>=x) j--;
if(i<j) input[i++]=input[j];
while(i<j && input[i]<=x) i++;
if(i<j) input[j--]=input[i];
}
input[i]=x;
return i;
}
void getLeastNumbers(int* input,int n,int* output,int k)
{
//有效性检测
if(input==NULL || output==NULL || n<=0 || k>n || k<=0) return;
int start=0,end=n-1;
int index=Partition(input,start,end);
while(index!=k-1)
{
if(index>k-1) //若得到正确位置的元素位置大于k-1,则需要在其左分区继续找k-1位置
{
end=index-1;
index=Partition(input,start,end);
}
else //若得到正确位置的元素位置小于k-1,则需要在其右分区继续找k-1位置
{
start=index+1;
index=Partition(input,start,end);
}
}
for(int i=0;i<k;i++) output[i]=input[i];
}
3.容器k:使用大小为k的数据容器存储最小的k个数字,遍历数组。
若容器未满时则填入容器
若容器满了,则比较容器中最大的数和遍历到的数字,若容器中最大的数小于遍历的数字则继续遍历,若大于则删除这个数字填入遍历的数字
这个容器的数据结构可以采用最大堆或者红黑树
面试题 31:连续子数组的最大和
解题思路:举例+动态规划
1.举例:我们可以遍历数组,从数组第一个元素开始,分别计算最大子数组的和和累加子数组的和
1.1累加子数组的和可以小于最大子数组的和,但若大于最大子数组的和就会刷新最大子数组的和
1.2最大子数组的和为遇到的子数组的最大值1
2
3
4
5
6
7
8
9
10
11
12
13
14
15int findGreastestSumOfSubArray(int* array,int length)
{
if(array==NULL || length<=0) throw new exception("input is invalid!");
int curSum=0;
//累加子数组初始化为最大负数,不能初始化为0,防止数组全为负数的情况
int greastestSum=0x80000000;
for(int i=0;i<length;i++)
{
if(curSum<=0) curSum=array[i]; //若此时累加子数组的和小于0,则重新初始化
else curSum=curSum+array[i]; //若此时累加子数组的和大于0,则加上当前值
if(curSum>greastestSum) greastestSum=curSum; //刷新最大子数组的和
}
return greastestSum;
}
2.动态规划:针对第i个数字结尾的子数组,当其前面的子数组的数字和小于0时,此时第i个数字结尾的子数组就是第i个数字本身,若前面的子数组所有数字大于0,则与其相加
面试题 32:从1到n整数中1出现的次数
解题思路:参考这里1
2
3
4
5
6
7
8public int NumberOf1Between1AndN_Solution(int n) {
int cnt = 0;
for (int m = 1; m <= n; m *= 10) {
int a = n / m, b = n % m;
cnt += (a + 8) / 10 * m + (a % 10 == 1 ? b + 1 : 0);
}
return cnt;
}
面试题 33:把数组排成最小的数
解题思路:比较规则+大数问题(字符串比较)
1.比较规则:若给出两个数字x、y,我们需要确定一个规则判断xy和yx哪个大,而不是比较x、y哪个大
2.大数问题(字符串比较):x、y为int,但是xy或者yx可能会溢出,因此这是一个隐形的大数问题,解决方法时将数字转换成字符串,此时比较xy和yx就可以按照字符串大小比较就可以了
3.字符串格式化:将格式化的数据写入字符串的函数sprintf(char* str,char* format[,argument]),str为被写入的字符串,format为格式化字符串,argument为被格式化的变量,常用将整数打印到字符串中,如
sprintf(s, “%d”, 123); 把整数123打印成一个字符串保存在s中
sprintf(s, “%8x”, 4567); 小写16进制,宽度占8个位置,右对齐1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41//数字最长位数
const int MaxNumberLength=10;
//自定义比较规则
int compare(const void* x,const void* y)
{
char* xy=new char[MaxNumberLength*2+1];
strcpy(xy,*(const char**)x); // 复制x到xy中
strcat(xy,*(const char**)y); //将y连接到xy后
char* yx=new char[MaxNumberLength*2+1];
strcpy(yx,*(const char**)y);
strcat(yx,*(const char**)x);
return strcmp(xy,yx); //比较字符串大小
}
void printMinNumber(int* numbers,int length)
{
//输入有效性检测
if(numbers==NULL || length<=0) return;
//用于保存字符数组的数组
char** strNumbers=(char**)(new int[length]);
//for循环将数字格式化存储至数组中
for(int i=0;i<length;i++)
{
strNumbers[i]=new char[MaxNumberLength+1];
sprintf(strNumbers[i],"%d",numbers[i]);
}
//对数组中的字符数组用自定义的规则排序
qsort(strNumbers,length,sizeof(char*),compare);
//格式化输出并释放空间
for(int i=0;i<length;i++)
{
cout<<strNumbers[i];
delete[] strNumbers[i];
}
delete[] strNumbers;
}
面试题 34:丑数
解题思路:空间换时间(创建数组保存已找到的丑数)
1.丑数特点:根据定义,丑数应该是另一个丑数乘2、3、5的结果
2.创建数组存储已找到的丑数:将数组的丑数排序,每一个丑数是前面的丑数乘以2、3、5得到的
3.丑数排序,已有数组的最大丑数设为M,将之前的每个丑数乘2中的大于M的最小值记作M2,乘3乘5的大于M的最小值记作M3、M5,则下一个丑数为M2、M3、M5中的最小值
4.优化:并不需要之前的每一个丑数都作乘法,只需要其找到其中的阈值T2,T3,T5,T前的丑数乘对应数字小于M,T后的丑数乘对应数字大于M1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26int getUglyNumber(int n)
{
if(n<0) return 0;
else if(n<=6) return n; //1,2,3,4,5,6均为丑数
int *uglyNumbers=new int[n]; //创建存储丑数的数组
uglyNumbers[0]=1;
int curNumber=1;
int t2=0,t3=0,t5=0; //阈值下标
while(curNumber<n)
{
int m2=uglyNumbers[t2]*2; //通过2的阈值下标找到2的阈值
int m3=uglyNumbers[t3]*3;
int m5=uglyNumbers[t5]*5;
int min=min(m2, min(m3, m5));
uglyNumbers[curNumber]=min; //最小的数存入数组
curNumber++;
if(min==m2) t2++; //最小的数属于乘2找到的,则2的阈值下标加1
if(min==m3) t3++;
if(min==m5) t5++;
}
int ugly=uglyNumbers[n-1];
delete[] uglyNumbers;
return ugly;
}
面试题 35:第一个只出现一次的字符
解题思路:哈希表
1.由于题目与字符有关,我们需要统计字符在字符串出现的次数,需要一个数据容器存放每个字符出现的次数,也就是说这个容器的作用是将一个字符映射成一个数字,哈希表正是这个用途
2.定义哈希表的键值(Key)为字符,而值(Value)为字符出现的次数
3.扫描字符串两次,第一次每扫描到一个字符就在哈希表对应项次数加1,第二次扫描出第一个出现1次的字符
4.实现哈希表:字符(char)是一个长度为8的数据类型,因此共有2^8=256种可能,于是可以创建一个长度为256的数组,每个字符根据其ASCII码值作为数组下标对应的数字是其出现的次数
5.时间复杂度:若字符串长度为n,第一次扫描的时间复杂度为O(n),第二次扫描的时间复杂度也是O(n),于是中的时间复杂度也是O(n)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23char firstCharInStr(char* str)
{
if(str==NULL) return '\0';
//创建哈希表
const int tableSize=256;
unsigned int hashTable[tableSize];
//初始化哈希表
for(unsigned int i=0;i<tableSize;i++)
hashTable[i]=0;
//第一次遍历,将遍历到的字符以字符的ASCII码作为下标的数组值加1
char* hashKey=str;
while(*(hashKey)!='\0')
hashTable[*(hashKey++)] ++;
//第二次遍历,找到第一个出现1次的字符
hashKey=str;
while(*(hashKey)!='\0')
{
if(hashTable[*hashKey]==1) return *hashKey;
hashKey++;
}
return '\0';
}
面试题 36:数组中的逆序对
解题思路:归并排序时统计
1.分解数组:将数组分解直至长度为1的子数组
2.统计、合并、排序数组:
统计数组:申明P1、P2指向两个子数组的头部,P3指向归并数组的头部,只有*P1>*P2时需要统计,逆序数统计数增加子数组P1到末尾的元素数量,因为*P1后的元素均大于*P1,于是均与*P2形成逆序对
合并数组:若*P1>*P2,统计完成后*P3=*P2,P2++,P3++,继续比较*P1和*P2;若P1<\P2,则无需统计,*P3=*P1,P1++,P3++,继续比较*P1和*P2
排序数组:合并完成的数组就是已经排序好的数组,排序数组是因为避免在下次的统计过程中重复统计1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42//不要使用count名,因为std空间下也有count变量会指代不明,若要使用则要用::count形式
int cnt=0;
int InversePairs(int* array,int length)
{
//有效性检测
if(array==NULL || length<=0) return 0;
//创建辅助空间
int* temp=new int[length];
split(array,0,length-1,temp);
delete[] temp;
return cnt;
}
//1.分解数组
void split(int* array,int start,int end,int* temp)
{
if(end-start<1) return;
int mid=start+(end-start)/2; //不要用(start+end)/2溢出风险
split(array,start,mid,temp);
split(array,mid+1,end,temp);
merge(array,start,mid,end,temp);
}
//2.统计合并排序数组
void merge(int* array,int start,int mid,int end,int* temp)
{
int p1=start,p2=mid+1,p3=start;
int k=0;
//合并数组
while(p1<=mid && p2<=end)
{
//有等于的情况则不能使用这个方法了
if(array[p1]<array[p2]) temp[k++]=array[p1++];
else {
cnt=cnt+mid-p1+1; //统计逆序对
temp[k++]=array[p++];
}
}
while(p1<=mid) temp[k++]=array[p1++];
while(p2<=end) temp[k++]=array[p2++];
//排序数组
for(int i=0;i<k;i++)
array[start+i]=temp[i];
}
面试题 37:两个链表的第一个公共节点
解题思路:公共结点链表特点+栈
1.若两个链表有公共结点,则它们公共结点后的节点是相同的,拓扑结构是Y而不是X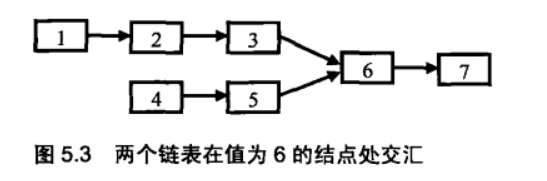
2.栈:因为公共结点后的节点是相同的,我们想从尾遍历两个链表,直到遍历到的节点不一样时,其后一个结点就是第一个公共节点,然而链表只能从前往后遍历,因此我们需要使用栈存储两个链表来实现从尾遍历链表
3.时间复杂度:若两个链表长度为m、n,则暴力破解时间复杂度为O(mn),栈遍历为O(m+n)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21static stack<ListNode*> list1,list2;
ListNode* findFirstCommonNode(ListNode* head1,ListNode* head2)
{
ListNode* l1=head1,l2=head2;
while(l1!=NULL){
list1.push(l1);
l1=l1->next;
}
while(l2!=NULL){
list2.push(l2);
l2=l2->next;
}
ListNode* firstCommonNode=NULL;
while(list1.top()==list2.top())
{
firstCommonNode=list1.top();
list1.pop();
list2.pop();
}
return firstCommonNode;
}
面试题 38:数字在排序数组中出现的次数
解题思路:二分查找法
1.由于输入数组是排序的,我们很自然想到利用二分查找算法
2.寻找数组中第一个数字k和最后一个数字k,它们的下标作简单的处理就能得出数组中有几个k
3.找第一个数字k和最后一个数字k可使用二分查找法,第一个k的特点是上一个数字小于k下一个数字等于k,最后一个k的特点是下一个数数字大于k上一个数字等于k
4.注意边界检测(k为第一个和最后一个元素)和有效性检测(k不在数组中)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32int getNumberOfK(int* array, int length, int k)
{
//有效性检测
if (array == NULL || length <= 0 || k<array[0] || k>array[length-1]) return 0;
int start = 0, end = length - 1;
int cur = (start+end)/ 2;
//找第一个k 注意边界检测 k为第一个元素
while (cur!=0 && cur!=length-1)
{
if (array[cur] == k && array[cur - 1]<k) break;
if (array[cur]<k) start = cur+1;
if (array[cur]>=k) end = cur-1;
cur = (start + end) / 2;
cout << "cur1:" << cur << endl;
}
int startK = cur;
start = 0;
end = length - 1;
cur = (start + end) / 2;
//找最后一个k 注意边界检测 k为最后一个元素
while (cur!=0 && cur!=length-1)
{
if (array[cur] == k && array[cur + 1]>k) break;
if (array[cur]<=k) start = cur+1;
if (array[cur]>k) end = cur-1;
cur = (start + end) / 2;
cout << "cur2:" << cur << endl;
}
int endK = cur;
return endK - startK + 1;
}
面试题 39:二叉树的深度
解题思路:递归分治
递归分治::用递归的思想遍历二叉树,用分治的思想理解二叉树某个节点的深度是max(左子树的深度,右子树的深度)+11
2
3
4
5int TreeDepth(BinaryTreeNode* root)
{
if(root==NULL) return 0;
return 1+max(TreeDepth(root->left),TreeDepth(root->right));
}
解题思路:后续遍历
后续遍历:我们在遍历某个节点时,已经遍历了它的左右子节点了,这时我们只需要根据它的左右子节点的深度判断这个节点是否平衡,并得到这个节点的深度,对于判断这个节点的父节点是不是平衡的有关键作用1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30bool IsBalancedTree(BinaruTreeNode* root)
{
int depth=0;
return IsBalanceNode(root,&depth);
}
bool IsBalanceNode(BinaruTreeNode* root,int* depth)
{
//遍历到叶子节点的子节点时,深度设为0,返回叶子节点
if(root==NULL)
{
*depth=0;
return true;
}
//左子树深度和右子树深度
int left,right;
//若左右子树平衡时,会返回左右子树的深度和true
if(IsBalanceNode(root->left,&left) && IsBalanceNode(root->right,&right))
{
//计算左右子树的深度差
int diff=left-right;
//深度差的绝对值在1以内 则平衡,返回这个节点的深度和true
if(diff<=1 && diff>=-1)
{
*depth=1+(left>right?left:right);
return true;
}
}
//若左右子树不平衡或者这个节点不平衡,直接返回false
return false;
}
面试题 40:数组中只出现一次的数字
解题思路:分治+异或运算
分治:先考虑数组中只有一个只出现一次的数字
异或运算:x不等于y,则x^y等于1;x等于y,则x^y等于0
异或求解思路:将数组的所有元素异或得到的结果为不存在重复的两个元素异或的结果
分治思路:两个不相等的元素在位级表示上必定会有一位存在不同,数组异或的结果为两个只出现一次元素异或的结果,只需要找到异或结果中最右侧不为0的位,可利用这一位区分出这两个数(这两个数这一位一定不等),之后将数组分为两个数组,分别求解出每个数组中不同的那个数即可1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17void FindNumOnce(int array[],int length,int* num1,int* num2)
{
//有效性检测
if(array==NULL || length<2) return;
//数组中所有数异或运算,得到只出现一次的两个元素异或的结果
int resultOR=0;
for(int i=0;i<length;i++) resultOR=resultOR^array[i];
//找到结果中最右侧不为0的位(即最右侧为1的位)
resultOR=resultOR & (-resultOR);
//将数组分成两个部分分别进行异或运算
*num1=*num2=0;
for(int i=0;i<length;i++)
{
if((array[i]&resultOR)==0) num1=num1^array[i];
else num2=num2^array[i];
}
}
面试题 41:和为S的两个数字/和为S的连续正数序列
解题思路:根据结果修正
根据结果修正:由于数组是排序的,因此可以根据两个数字的和与S大小比较调整组成元素的大小
具体实现:申明两个指针start、end指向数组头和尾,若指针所指元素的和下于S,则证明需要增大和,则可以start++,因为数组是排序的,所以array[++start]>array[start],若和小于S,则需要减小和,可以end–,同理因为array[–end]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21bool FindNumberWithSum(int array[],int length,int sum,int* num1,int* num2)
{
bool result=false;
//有效性检测
if(array==NULL || length<2 || num1==NULL || num2==NULL || sum>2*array[length-1] || sum<2*array[0]) return result;
int start=0,end=length-1;
while(start<end)
{
if(array[start]+array[end]<sum) start++;
if(array[start]+array[end]>sum) end--;
if(array[start]+array[end]==sum)
{
*num1=array[start];
*num2=array[end];
result=true;
break;
}
}
return result;
}
解题思路:根据结果修正
根据结果修正:由于数组是排序的,因此可以根据包含的数字的和与S比大小调整包含元素多少
具体实现:申明两个指针start、end指向数组第一二个元素,若和小于S,则end++,包含多一个元素增大和,若和大于S,则start++,剔除最小的元素减小和,若和等于S,打印序列并且end++继续遍历1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26void FindSumInSequence(int sum)
{
if(sum<3) return;
int start=1,end=2,curSum=3;
int middle=(sum+1)/2;
while(start<=middle && end<sum)
{
if(curSum>sum)
{
curSum=curSum-start; //和减小
start++;
}
if(curSum<sum)
{
end++;
curSum=curSum+end; //和增加
}
if(curSum==sum)
{
for(int i=start;i<=end;i++) cout<<i<<ends;
cout<<endl;
end++;
curSum=curSum+end; //和增加
}
}
}
面试题 42:反转单词顺序/左旋转字符串
解题思路:反转句子+反转单词1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39void reverseStr(char* str,int start,int end)
{
while(start<end)
{
char temp = str[start];
str[start] = str[end];
str[end] = temp;
start++;
end--;
}
}
void ReverseStentence(char *str)
{
if(str==NULL) return;
int start=0;
int end=0;
while(str[end]!='\0') end++;
end--;
reverseStr(str,start,end);
start=end=0;
while(str[end]!=' ') end++;
end--;
reverseStr(str,start,end);
while(str[start]=='\0')
{
while(str[start]!=' ' && str[start]!='\0') start++;
if(str[start]==' ')
{
start++;
end=start;
while(str[end]!=' ' && str[end]!='\0') end++;
end--;
reverseStr(str,start,end);
}
}
}
解题思路:三次反转
上一题加入字符串是”abc def”,翻转后成为了”def abc”,相当于把前面三个字符串移到后面去了,类似地,这一题我们也可以如此,如给定”abcxyz”,将K(假设K=3)位左移,变成了”xyzabc”,也可以采取上一题的解法
1.字符串分成两部分(前K位和后面位):即”abc”和”xyz”
2.两部分分别反转:即”cbazyx”
3.整体字符串反转:即”xyzabc”,前K位就移至后面了1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27void reverseStr(char* str,int start,int end)
{
while(start<end)
{
char temp = str[start];
str[start] = str[end];
str[end] = temp;
start++;
end--;
}
}
void LeftRotateStr(char* str,int n)
{
if (str == NULL || n <= 0) return;
int length = 0;
while (str[length] != '\0') length++;
if (n >= length) return;
int start = 0;
int end = n - 1;
reverseStr(str, start, end);
start = n;
end = length - 1;
reverseStr(str, start, end);
start = 0;
end = length - 1;
reverseStr(str, start, end);
}
面试题 43:n个骰子的点数
解题思路:动态规划(递归/迭代)
动态规划:将问题分为不同的阶段的问题,根据开始阶段已知的问题答案,逐步推到出最终答案,通常基于一个递归公式(状态转移方程)和一个或者多个初始状态
1.确定问题解的表达形式:用f(n,s)表示n个骰子点数和为s的排列情况总数
2.递归公式:将骰子分为1个和n-1个,1个骰子的点数为1-6,若n个骰子点数和为s,则根据1个骰子的点数不同,n-1个骰子的点数也不同,因此有状态转移方程:
f(n,s)=f(n-1,s-1)+f(n-1,s-2)+f(n-1,s-3)+f(n-1,s-4)+f(n-1,s-5)+f(n-1,s-6) ,0
3.初始状态:n=1时,f(1,1)=f(1,2)=f(1,3)=f(1,4)=f(1,5)=f(1,6)=1
递归版本:简洁、低效1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21int getSumCount(int n,int sum)
{
//有效性检测,骰子至少为1个,点数和在n-6n之间,否则排列情况数量为0
if(n<1 || sum<n || sum>6*n) return 0;
//初始状态
if(n==1) return 1;
//状态转移方程
int sumCount=0;
sumCount=getSumCount(n-1,sum-1)+getSumCount(n-1,sum-2)+
getSumCount(n-1,sum-3)+getSumCount(n-1,sum-4)+
getSumCount(n-1,sum-5)+getSumCount(n-1,sum-6);
return sumCount;
}
void printAllSumCount(int n)
{
//i为n个骰子出现点数和s的所有可能
//若需要打印出概率可将结果除以6^n
for(int i=n;i<=6*n;i++) cout<<"fn("<<n<<","<<i<<")="<<getSumCount(n,i)<<endl;
}
迭代版本:从底层开始、高效1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34void getSumCount(int n,int* count)
{
if(n<1) return;
//初始状态
count[0]=count[1]=count[2]=count[3]=count[4]=count[5]=1;
if(n==1) return;
//从骰子数量为2迭代到骰子数量为n
for(int i=2;i<=n;i++)
{
//针对骰子数量为i,点数和sum有i到6i种排列可能
for(int sum=6*i;sum>=i;sum--)
{
//针对骰子和为sum,将骰子数量i分为1个和i-1个
//1个骰子点数可以为1、2、3、4、5、6
//i-1个骰子的点数和在上次迭代的数组中
int minus1=(sum-1-(i-1))>=0?count[sum-1-(i-1)]:0;
int minus2=(sum-2-(i-1))>=0?count[sum-2-(i-1)]:0;
int minus3=(sum-3-(i-1))>=0?count[sum-3-(i-1)]:0;
int minus4=(sum-4-(i-1))>=0?count[sum-4-(i-1)]:0;
int minus5=(sum-5-(i-1))>=0?count[sum-5-(i-1)]:0;
int minus6=(sum-6-(i-1))>=0?count[sum-6-(i-1)]:0;
count[sum-i]=minus1+minus2+minus3+minus4+minus5+minus6;
}
}
}
void printAllSumCount(int n)
{
//共有n-6n种排列组合可能,用5n+1大小的数组存储
int* count=new int[5*n+1]
//将参数1后的参数2大小空间初始化为参数3
memset(count,0,(5*n+1)*sizeof(int));
getSumCount(n,count);
}
面试题 44:扑克牌顺子
解题思路:三重处理
第一重处理:排序
第二重处理:统计0个数
第三种处理:统计数组是否连续,若不连续统计空缺数,小于等于0的个数则连续1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22bool isContinuous(int* numbers,int length)
{
if(numbers==NULL || length!=5) return false;
//排序
qsort(numbers,length,sizeof(int),compare);
//统计0的个数
int numOfZero=0;
for(int i=0;i<length;i++) if(numbers[i]==0) numOfZero++;
//统计数组是否连续和空缺数
int numOfGap=0;
for(int i=numOfZero;i<length;i++)
{
if(numbers[i]+1==numbers[i+1]) continue;
else if(numbers[i]+2==numbers[i+1]) numOfGap++;
else if(numbers[i]+3==numbers[i+1]) numOfGap=numOfGap+2;
else return false;
}
if(numOfGap<=numOfZero) return true;
return false;
}
面试题 45:圆圈中最后剩下的数字
解题思路:环形链表模拟圆圈1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37struct ListNode
{
int val;
ListNode* next;
};
int LastLeftNumber(int n,int m)
{
if(n<1 || m<1) return -1;
if(m==1) return 0;
//利用数组构造环形链表(不可用循环定义链表,无法命名)
ListNode* array=new ListNode[n];
array[n-1]=new ListNode;
array[n-1]->val=n-1;
for(int i=n-2;i>=0;i--)
{
array[i]=new ListNode;
array[i]->val=i;
array[i]->next=array[i+1];
}
array[n-1]->next=array[0];
//开始删除操作(删除结点的前一个结点next删除结点后一个结点即可)
ListNode* cur=array[0];
for(int i=0;i<=n-2;i++)
{
int jump=m-2;
while(jump!=0)
{
cur=cur->next;
jump--;
}
cur->next=cur->next->next;
cur=cur->next;
}
return cur->val;
}