本文主要用来系统归纳并总结所遇到的算法及其实现方法

大纲
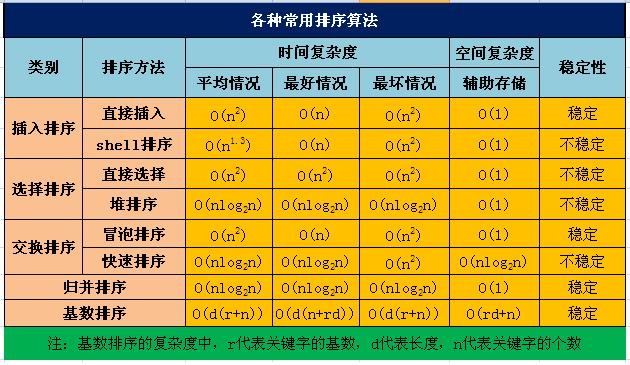
算法复杂度
1.冒泡排序
原始版本:冒泡排序思想(从小到大):
- 1.比较相邻的前后两个数据,若前面的数据大于后面的数据,就交换两个数据位置
- 2.对数组第0个数据到N-1个数据进行一次遍历后,第N-1位置上的就为最大的数据
- 3.N=N-1,若N!=0则对剩下的数组执行12步,否则排序完成改良1:冒泡排序比较刻板,有时候已经排序好了缺还继续遍历,导致后面的多次遍历都是读取值不交换,浪费了时间,因此我们可以改良一下,设置一个标志,若有一次遍历没有发生交换,则表示排序完成
1
2
3
4
5
6
7
8
9void bubbleSort(int a[],int n)
{
for(int i=0;i<n;i++) //i表示整体遍历次数,即排好数据的个数
for(int j=1;j<n-i;j++) //j表示每次的比较遍历,每完成一次i就减少j遍历的域一个,因此j只遍历到n-i
if(a[j-1]>a[j]) Swap(a[j-1],a[j]);
}
//Tips:若用j与j+1比较,则内部循环为
//for(int j=0;j<n-i-1;j++)
// if(a[j]>a[j+1]) Swap(a[j],a[j+1]); - 1.外层循环不再以整体遍历次数作为循环结束条件,而是以是否交换的标志作为循环结束条件
- 2.控制内层循环还是需要使用i作为整体循环次数,减少遍历已经排好位置的值的多余遍历改良2:若每次进行遍历时,后面部分的数组已经排好序了且都大于前面的数组,在每次遍历就只需要遍历前面的数组即可,我们可以记录最后交换的位置确定下次循环的范围,下次循环到这个位置即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17void bubbleSort(int a[],int n)
{
bool signal=true;
int i=0; //排好数据的个数
while(signal) //1.
{
signal=false;
for(int j=1;j<n-i;j++) //2.
if(a[j-1]>a[j])
{
Swap(a[j-1],a[j]);
signal=true;
}
i++; //2.
}
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17void bubbleSort(int a[],int n)
{
int signal=n; //最后交换的位置
int i; //排好数据的个数
while(signal>0) //1.
{
i=signal;
signal=0; //signal初始化为0,因为一开始交换的位置不知道
for(int j=1;j<i;j++)
if(a[j-1]>a[j])
{
Swap(a[j-1],a[j]);
signal=j; //记录最后交换的位置
}
}
}
2.插入排序
基本思想:每次将一个待排序的值插入到已排序的序列中的正确位置,直到全部记录插入完成
原始版本:由小到大
- 1.初始时数组第一个数组成了已排序序列
- 2.搜索过程:将待排序的值与已排序的序列比较,找到其正确位置
- 3.数据后移过程:将大于待排序的值的数向后移一个单位,空出位置填入待排序的值改良1:原始版本3个for循环太不清晰简洁,将搜索与数据后移过程合并可减少一个循环
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21void insertSort(int a[],int n)
{
int i,j,k;
for(int i=1;i<n;i++) //1.从i=1开始遍历
{
for(j=i-1;j>=0;j--) //2.搜索过程
{
if(a[j]<a[i]) break;
}
if(j!=i-1) //若找到合适位置(若j=i-1则这个值已排好序)
{
int temp=a[i];
for(k=i-1;k>j;k--) //3.数据后移过程
{
a[k+1]=a[k];
}
a[j+1]=temp;
}
}
} - 1.待排序的值大于已排序序列中的最大值(最后一位),则无需插入
- 2.搜索+数据后移:搜索的时候将已排序序列值与待排序的值比较,若大则往后移,直到找到比待排序的值小的值,此时直接插入其后一位即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17void insertSort(int a[],int n)
{
int i,j;
for(i=1;i<n;i++)
{
if(a[i]<a[i-1]) //1.判断是否需要插入排序
{
int temp=a[i]; //保存待排序的值
for(j=i-1;j>=0;j--)
{
if(a[j]>temp) a[j+1]=a[j]; //若已排序序列的值比待排序的值大,则后移
else break; //若已排序序列的值比待排序的值小,则停止循环
}
a[j+1]=temp; //直接插入其后一位
}
}
}
3.选择排序
基本思想:与插入排序类似,都将数据分为有序区和无序区,不同的是,插入排序是将无序区第一个元素直接插入有序区形成更大的有序区,选择排序是从无序区选择最小(大)的元素放入有序区的最后
原始版本:
- 1.无序区最大数的下标初始化为有序区的最大数下标,便于写循环函数,若初始化为无序区第一个数下标,则循环从无序区第二个数开始
- 2.交换函数最好使用中间变量,因为有可能自己与自己交换,不使用中间变量需判断
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28void selectSort(int a[],int n)
{
int i,j,maxIndex;
for(i=0;i<n;i++)
{
maxIndex=i; //1.
for(j=i+1;j<n;j++)
{
if(a[j]>a[maxIndex]) maxIndex=j;
}
Swap(a[i],a[maxIndex]);
}
}
void Swap(int &a,int &b) //2.使用中间变量无需判断
{
int c=a;
a=b;
b=c;
}
void Swap(int $a,int &b) //2.不使用中间变量需判断
{
if (a != b)
{
a ^= b;
b ^= a;
a ^= b;
}
}
4.希尔排序
基本思想:实质是分组插入排序,先将待排序元素分割成若干个子序列(相隔某个增量),分别进行插入排序,然后依次缩小增量再进行排序,最后对全体元素进行插入排序,由于此时序列的有序程度已经很高了,因此效率较高
原始版本:
- 1.计算步长:通常是数组长度/2
- 2.确定分组个数:从0到一个步长的元素个数为分组个数,这些元素都是分组中的第一个元素
- 3.每个分组进行插入排序(两个for循环)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24void shellSort(int a[],int n)
{
int i,j,gap,k;
for(gap=n/2;gap>0;gap=gap/2) //1.计算步长
{
for(i=0;i<gap;i++) //2.确定分组个数
{
for(j=i+gap;j<n;j=j+gap) //3.每个分组进行插入排序
{
if(a[j]<a[j-gap])
{
int temp=a[j];
for(k=j-gap;k>=0;k=k-gap)
{
if(a[k]>temp) a[k+gap]=a[k];
else break;
}
a[k+gap]=temp;
}
}
}
}
}
5.归并排序
归并排序是基于分治法,基本思想是
归:将数组一直拆分,直到拆分成一个数据的时候,可以认为这个子数组为有序的
并:若两个子数组均有序,按顺序合并成一个数组就是有序的
原始版本:
- 1.合并函数:设定两个指针指向两个已排序数组的起始位置,比较指针所指元素,选择小的元素放入合并空间中并移动指针到下一个位置,若某一指针超出自身子数组的序列范围,则将另一子数组剩下所有元素赋值到合并序列中,最后将合并序列的元素覆盖原先数组元素的位置
- 2.分解函数:将传入的数组分解成两个数组,之后继续分解分解出来的两个子数组,直到分解出来的数组中仅有一个元素则可认为有序,之后调用合并函数合并子数组
- 3.归并排序:先申请空间,用来存放合并序列,调用分解函数后释放空间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39void mergeArray(int a[],int start,int mid,int end,int temp[]) //1.合并函数
{
int i=start,j=mid+1; //两个子数组的头元素
int m=mid,n=end; //两个子数组的尾元素
int k=0; //temp数组所赋值的位置
while(i<=m&&j<=n)
{
if(a[i]<a[j]) temp[k++]=a[i++];
else temp[k++]=a[j++];
}
while(i<=m) temp[k++]=a[i++];
while(j<=n) temp[k++]=a[j++];
for(i=0;i<k;i++)
{
a[start+i]=temp[i];
}
}
void splitArray(int a[],int start,int end,int temp[]) //2.分解函数
{
if(start<end)
{
int mid=(start+end)/2;
splitArray(a,start,mid,temp);
splitArray(a,mid+1,end,temp);
mergeArray(a,start,mid,end,temp);
}
}
bool mergeSort(int a[],int n) //3.归并排序
{
int *p = new int[n];
if(p==NULL) return false;
splitArray(a,0,n-1,p);
delete[] p;
return true;
}
6.快速排序
快速排序基于分治法
剑指offer上给出的是分区(Partition)方法是
- 1.随机找基准值
- 2.将基准值移至数组尾部
- 3.从数组头部开始遍历数组,找到一个小于基准值的数就将其移到数组前方
- 4.将基准值移到最后一个小于基准值的数的下一个位置上
- 5.返回基准值位置
之后便是快速排序(QuickSort):
- 1.若传入数组为一个数,则表示排序完成
- 2.否则调用分区(Partition)函数
- 3.分区完成后,对于左分区(小于基准值)右分区(大于基准值)再递归调用快速排序(QuickSort)方法,直到排序完成
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38//分区(Partition)
int Partition(int data[], int length, int start, int end)//分区
{
if(data==NULL || length<=0 || start<0 || end>=length) //输入参数有效行检验
throw new std::exception("Invalid Parameters");
int index = RandomInRange(start,end); //1.随机找基准值
Swap(&data[index], &data[end]); //2.将基准值移至数组尾部
int small = start-1; //small位置表示小于基准数的值要填入的位置
//3.从数组头部开始遍历数组,找到一个小于基准值的数就将其移到数组前方
for(index=start; index<end; index++)
{
if(data[index]<data[end]) //如果找到一个小于基准数的值
{
small++; //先small++找到应该放入数组的位置
if(small!=index) Swap(&data[index], &data[small]);
//若small位置等于index位置,证明index位置的值是处于正确位置上不需要交换
//否则证明index位置上的值小于基准数还不处于应该填入的位置上,需要交换到small位置上
}
}
small++;
Swap(&data[small], &data[end]); //4.将基准值移到最后一个小于基准值的数的下一个位置上
return small; //5.返回基准值位置,此时small左边为小于基准数的值,small右边为大于基准数的值
}
//快速排序(QuickSort)
void QuickSort(int data[],int length,int,start,int end)
{
if(start==end) return; //1.若传入数组为一个数,则表示排序完成
int index=Partition(data,length,start,end); //2.否则调用分区(Partition)函数
3.分区完成后,对于左分区(小于基准值)右分区(大于基准值)再递归调用快速排序(QuickSort)方法,直到排序完成
if(index>start) QuickSort(data,length,start,index-1);
if(index<end) QuickSort(data,length,index+1,end);
}
MoreWindows博客大大提出了另一种实现方法,较为简洁,与剑指Offer提出的实现方法相比,有如下改动
- 1.直接选取第一个数作为基准数(也可以随机选择)
- 2.有前后指针同时遍历数组,而不是单一从前往后遍历
- 3.采用挖坑填数思想:将基准数保存,之后尾指针遍历,若是所指向的值比基准数小则填入头指针所指向的位置,之后头指针遍历,若是所指向的值比基准数大则填入尾指针所指向的位置,直到头指针与尾指针指向同一个位置,在这个位置填入基准数即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24//快速排序
void quick_sort(int s[], int l, int r) //l为头指针,r为尾指针
{
if (l < r) //递归停止条件:若l=r即为数组只有一个元素时则停止递归
{
//Swap(s[l], s[RandomInRange(l,r)]); //1.直接选取第一个数作为基准数(也可以随机选择)
int i = l, j = r, x = s[l]; //将基准数保存在x里面,i为头指针,j为尾指针
while (i < j)
{
while(i < j && s[j] >= x) // 从尾向头找第一个小于基准数的数
j--;
if(i < j) // 填入头指针所指向的位置并头指针指向下一个位置
s[i++] = s[j];
while(i < j && s[i] < x) // 从头向尾找第一个大于等于x的数
i++;
if(i < j) // 填入尾指针所指向的位置并尾指针指向下一个位置
s[j--] = s[i];
}
s[i] = x; //将基准数填入头尾指针所指向的位置
quick_sort(s, l, i - 1); // 将左分区递归调用排序
quick_sort(s, i + 1, r); // 将右分区递归调用排序
}
}
Python实现更加简单,因为python在分治中很容易找到比基准值大或者小的数并放在一个数组里,而且Python合并数组也十分简单1
2
3
4
5
6
7
8
9//Python实现快速排序
def quicksort(array):
if(len(array)<2):
return array
else:
pivot=array[0]
less=[i for i in array[1:] if i <= pivot]
greater=[i for i in array[1:] if i> pivot]
return quicksort(less)+[pivot]+quicksort(greater)
7.堆排序
二叉堆:是完全二叉树或者近似完全二叉树,满足两个特点
- 1.父节点的键值总是大于(小于或者等于)任何一个子节点的键值,是一个最大堆(最小堆)
- 2.每个节点的左子树和右子树都是一个二叉堆
堆的存储:从上到下、从左到右遍历堆存储,一般用数组存储,这样节点有这样的规律:
对于i节点:其父节点下标为(i-1)/2,其左右子节点为2*i+1和2\i+2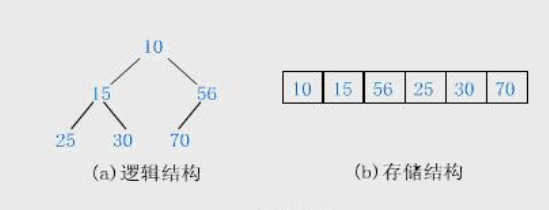
插入堆:总是将插入的数据放在数组最后,可通过将其与父节点比较调整位置,从而让数组满足堆的条件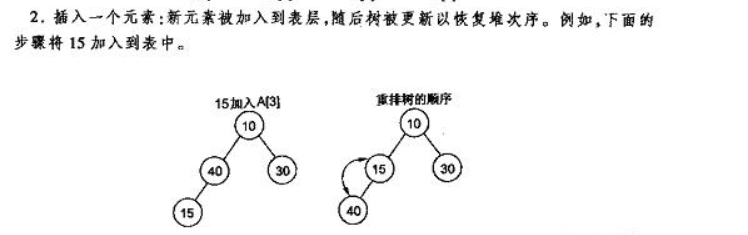
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17void insertHeap(int a[],int n,int newData)
{
a[n]=newData; //将插入的数据放在数组最后
int j=n; //子节点下标
int i=(j-1)/2; //父节点下标
while(i >=0 && j !=0)
{
//若父节点的值大于子节点,则交换并继续比较新的父节点与子节点(最小堆)
if(a[i]>a[j])
{
Swap(a[i],a[j]);
j=i; //交换后的父节点变新的子节点
i=(j-1)/2 //新的子节点的父节点
}
else break; //若父节点的值小于等于子节点,则停止交换
}
}
删除堆:按照定义每次只能删除第0个数据,为了便于重建堆,实际是将最后一个数据的值赋给根节点,再将根节点与其子节点比较调整位置,从而让数组满足堆的条件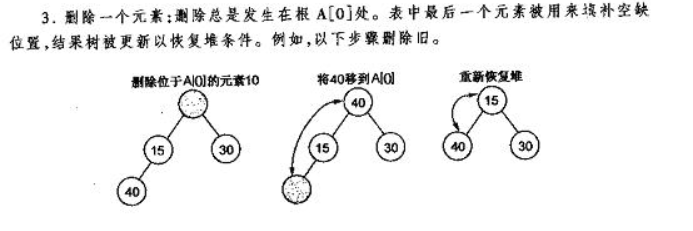
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18void deleteHeap(int a[],int n)
{
Swap(a[0],a[n-1]); //最后一个数据的值赋给头节点,此时尾节点下标为n-2
int i=0; //父节点下标
int j=2*i+1; //左子树节点
while(j<=n-2)
{
if(j+1<=n-2 && a[j+1]<a[j]) j++; //在左右子树节点找到最小的
//若父节点的值大于子节点,则交换并继续比较新的父节点与子节点(最小堆)
if(a[i]>a[j])
{
Swap(a[i],a[j]);
i=j; //交换后的子节点变为新的父节点
j=2*i+1; //新的父节点的子节点
}
else break; //若父节点的值小于等于子节点,则停止交换
}
}
堆化数组:只要将非叶子节点从下往上从右往左遍历,进行下沉调整即可
下沉函数:类似于删除堆中的操作,即父节点其子节点比较调整位置,从而让数组满足堆的条件1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24//下沉函数
void sink(int a[],int i,int n) //参数:数组,需要调整的父节点,数组长度
{
int j=2*i+1;
while(j<=n-1)
{
if(j+1<=n-1 && a[j+1]<a[j]) j++;
if(a[i]>a[j])
{
Swap(a[i],a[j]);
i=j;
j=2*i+1;
}
else break;
}
}
//建立最小堆
void makeHeap(int a[],int n)
{
for(int i=n/2-1;i>=0;i--)
{
sink(a,i,n);
}
}
堆排序:建立好的最小堆中第0个数据时堆中最小的数据,取出这个数据再执行下堆的删除,这样堆中第0个数据又是最小的数据,重复上述步骤直到堆中只有一个数据就直接取出,则取出的数据就是有序序列了1
2
3
4
5
6
7
8void heapSort(int a[],int n)
{
for(int i=n-1;i>0;i--)
{
makeHeap(a,i+1);
deleteHeap(a,i+1);
}
}